航空機や自動車を設計する際には部材の最適な形状を決めなければなりません.そのためには部材の強度を正確に予測する方法が必要であります. 本研究室では強度評価法に関する以下の研究を行っています。

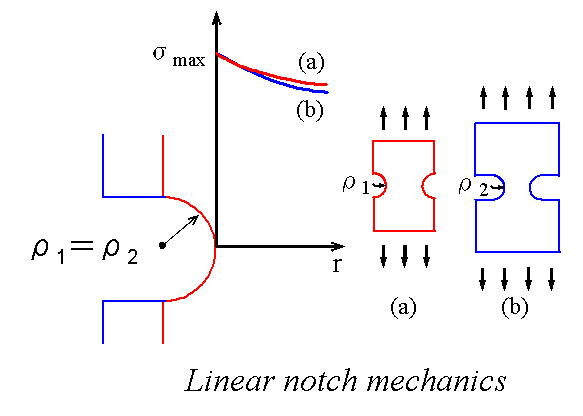
線形切欠き力学は,上図に示すように,形状が急激に変化した部分(切欠き)を有する二つの部材で,切欠き半径と切欠き底の最大応力を一致させれば, 切欠き底近傍の応力場が互いにほぼ一致することに基づいており,切欠きを有する部材の強度予測に有効な手法です. この方法を用いて,本研究室では切欠きを有する部材に,繰返し荷重が加わった場合の疲労強度予測に関する研究を行っています.
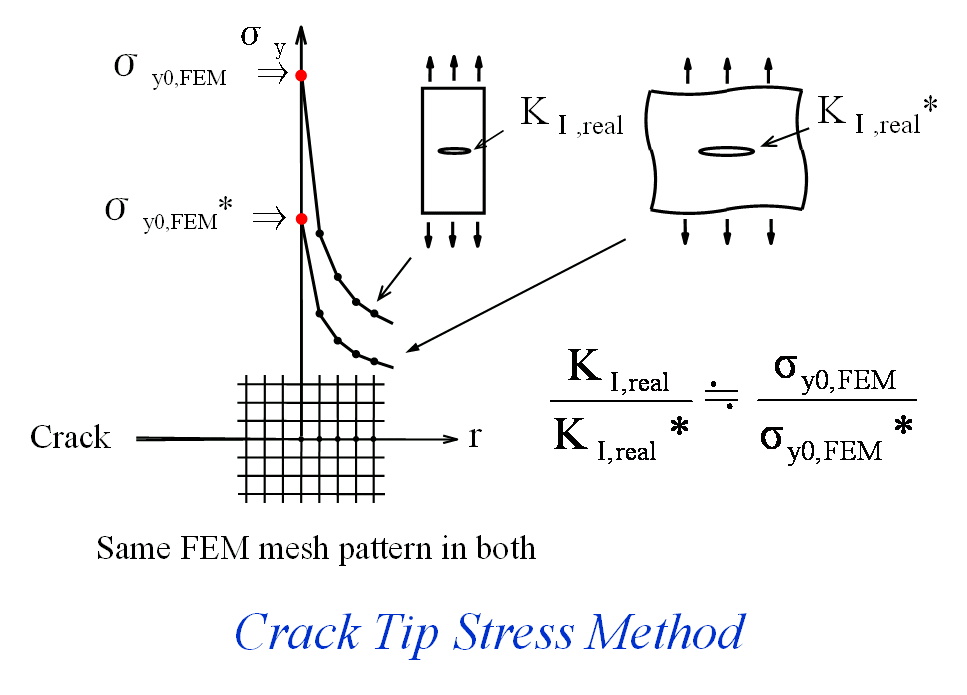
第ゼロ節点法は,有限要素法で得られるき裂先端の応力値がき裂先端近傍の応力場を忠実に代表することを原理としている. すなわち,上図に示すようにき裂を有する二つの部材において,き裂先端近傍の要素分割を合わせれば,有限要素法で得られる き裂先端の応力値の比と応力拡大係数の比がほぼ一致することを利用するものである.
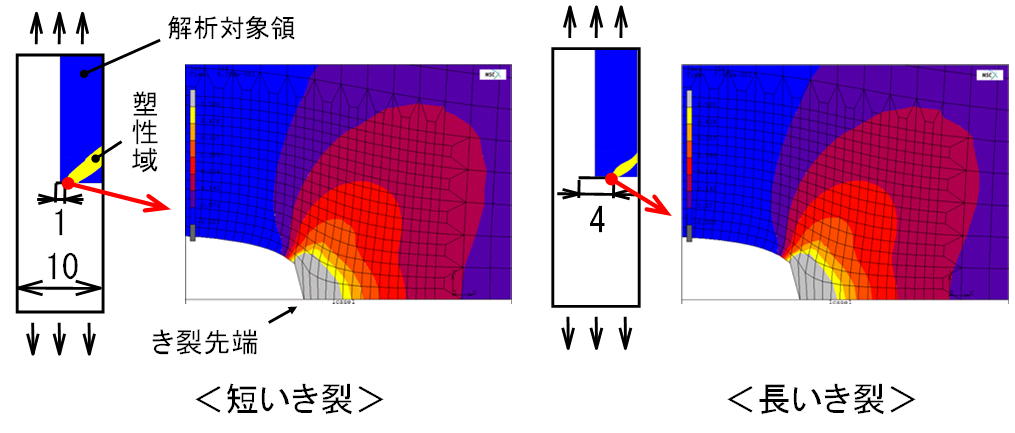
非線形き裂力学は,上図に示すようにき裂長さの異なる二つの部材において,有限要素法で得られるき裂先端の塑性ひずみの値を揃えれば,
き裂先端近傍のき裂開口形状と塑性ひずみ分布がほぼ一致することに基づくものです(ただしこの際に,き裂先端近傍の要素分割は両部材で一致させるものとします).
なお,有限要素法の解析結果は現実とは異なりますが,二つの部材の条件を揃えて有限要素解析を行えば,同一現象を保証する尺度と成ります.
本研究室ではこの方法を各種き裂問題に適用し,その適用方法や適用限界などについて研究しています.
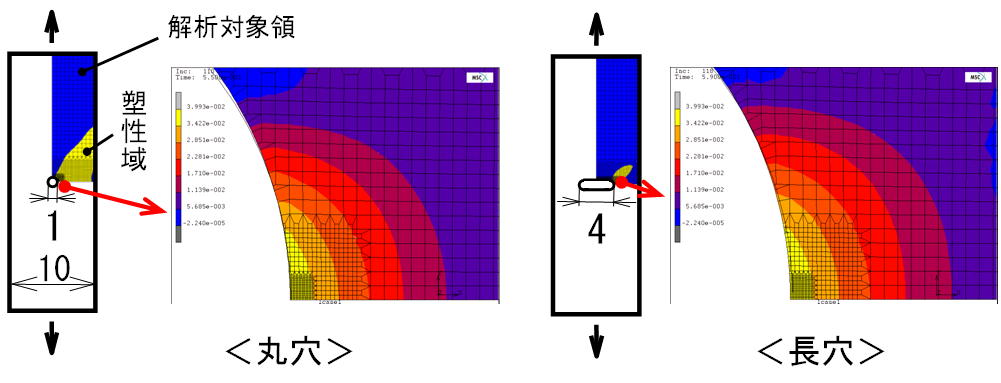
非線形切欠き力学は,切欠き半径が同じで,切欠き深さの異なる二つの部材において,有限要素法で得られる切欠き底の塑性ひずみの値を揃えれば,
上図に示しているように切欠き底近傍の変形と塑性ひずみ分布がほぼ一致することに基づくものです
(ただしこの際に,切欠き底近傍の要素分割は両部材で一致させなければいけません).
本研究室ではこの方法を各種切欠き問題に適用し,その適用方法や適用限界などについて研究しています.